
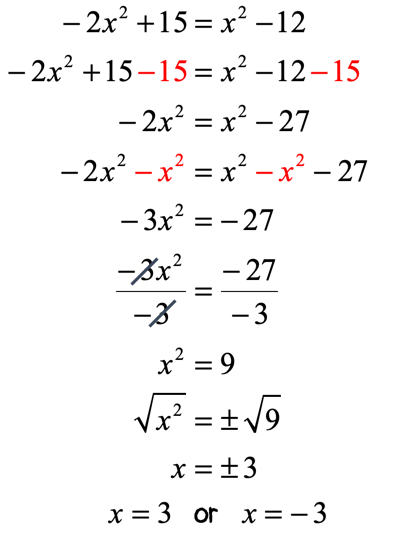
Void solve_quadratic (double a, double b, double c, double *x0, double *x1)ĭouble q = -0.5 * (b + copysign (sqrt (diff_of_products (b, b, 4.0*a, c)), b)) Provided the discriminant b²-4ac is positive With this building block, the real roots of a quadratic equation can be computed with high accuracy as follows, provided the discriminant is positive: /* compute the real roots of a quadratic equation: ax² + bx + c = 0, 284,ĭouble diff_of_products (double a, double b, double c, double d) If it cannot be factored quickly, solve by completing the square or the. "Further Analysis of Kahan's Algorithm for the Accurate Computation Choose the Best Method to Solve a Quadratic Equation Try solving by factoring.

This provides for the efficient computation of ab-cd as follows: /*ĭiff_of_products() computes a*b-c*d with a maximum error <= 1.5 ulpĬlaude-Pierre Jeannerod, Nicolas Louvet, and Jean-Michel Muller,

This allows the accurate computation of the product of two native-precision floating-point numbers as the unevaluated sum of two native-precision floating-point numbers, without resorting to the use of extended-precision arithmetic in intermediate computation: h = a * b and l = fma (a, b,- h) where h+l represents the product a*b exactly. Our main goal is to review traditional textbooks methods and offer an alternative, often side-stepped method based on the.
Methods for solving quadratic equations full#
Note that on platforms without hardware support for FMA, fma() must use emulation, which is often quite slow, and some emulations have been found to have serious functional deficiencies.įMA computes a*b+c using the full product (neither rounded nor truncated in any way) and applies a single rounding at the end. In this paper we explore different ways of solving quadratic equations. It is exposed in C/C++ as a standard math function fma(). This makes use of the fused multiply-add operation, or FMA, which is available on almost all modern processors including x86-64, ARM64, and GPUs. Recent follow-up work to Kahan's note looked at the more general issue of computing the difference of two products ab-cd:Ĭlaude-Pierre Jeannerod, Nicolas Louvet, Jean-Michel Muller, "Further analysis of Kahan's algorithm for the accurate computation of 2 x 2 determinants." Mathematics of Computation, Vol. William Kahan, "On the Cost of Floating-Point Computation Without Extra-Precise Arithmetic", Nov. It is examined in detail in the following research note: The question indicates an awareness of the problem of subtractive cancellation when the commonly used mathematical formula is applied directly using floating-point arithmetic, and the techniques to work around it.Īn additional issue to be considered is the accurate computation of the term b²-4ac. This answer assumes that the primary concern here is robustness with regard to accuracy, rather than robustness with regard to overflow or underflow in intermediate floating-point computations. If the quadratic equation is of the form ax + bx + c 0, where a 0 and the quadratic expression is not factorable, try completing the square.


 0 kommentar(er)
0 kommentar(er)
